Bellman Expectation Equation
이전 Chapter에서 MDP(Markov Decision Process)와 Value function에 대해서 살펴보았습니다. Agent는 이 value function을 가지고 자신의 행동을 선택하게 됩니다. value function에는 두 가지가 있는데 다음과 같이 정의됩니다.

Bellman equation for Value function
Value function의 정의에서 value function은 다음과 같이 풀어써볼 수 있습니다. Return의 정의에 따라 풀어쓴 다음에 discount ratio로 묶어주면 아래와 같은 식이 됩니다. 아래와 같이 다음 state와 현재 state의 value function 사이의 관계를 식으로 나타낸 것을 Bellman equation이라고 합니다.

policy를 포함한 value function과 action value function도 Bellman equation의 형태로 아래와 같이 표현할 수 있습니다.

하지만 위와 같이 expectation으로 표현하는 것은 조금은 추상적이며 직관적이지 않을 수도 있습니다. 같은 식을 다른 방법으로 표현할 수도 있습니다. 현재 state의 value function과 next state의 value function의 상관관계의 식을 구하려면 그 사이에 있는 state-action pair(어떤 state에서 어떤 행동을 한 상태를 하나의 state같이 생각하는 개념)에 대해서 그 관계를 나눠볼 필요가 있습니다.
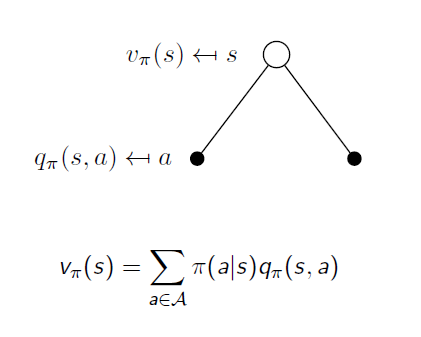
첫 번째로는 위와 같이 state와 state-action과 관계를 생각해 볼 수 있습니다. 흰 점은 state를 나타내고 검은 점은 state에서 action을 선택한 상황을 의미합니다. 간단히 표현하고자 그림에서는 가지를 2개씩만 쳤는데 이보다 더 많을 수도 적을 수도 있습니다. state에서 뻗어나가는 가지는 각 각의 action의 개수만큼입니다. 이때 V와 q의 관계는 policy로서 위 식처럼 표현이 가능합니다. 각 action을 할 확률과 그 action을 해서 받는 expected return을 곱한 것을 더하면 현재 state의 value function이 된다는 것입니다.
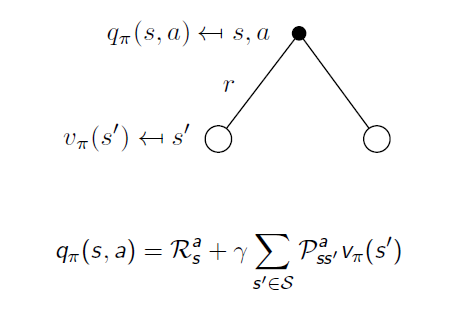
위 그림보다 추가된 것은 r인데 reward를 의미합니다. reward의 정의에 state와 action이 모두 조건으로 들어가기 때문에 그림에서 검은 점 밑에 표시된 것을 볼 수 있습니다. 또한 action에서 퍼져나가는 가지는 만약 deterministic한 환경이라면 하나의 가지일 것이나 앞에서도 말했듯이 외부적인 요인에 의해서(바람이 분다던지) 같은 state에서 같은 action을 해줘도 다른 state로 갈 수도 있습니다. 그러한 확률을 전에 언급했듯이 state transition probability matrix라고 합니다. action-value function은 imediate reward에다가 action을 취해 각 state로 갈 확률 곱하기 그 위치에서의 value function을(한 step이 지났으므로 discounted됩니다) 더한 것으로 표현할 수 있습니다.
이 두 도표를 합치면 아래와 같이 되고 식으로는 다음과 같이 표현할 수 있습니다.
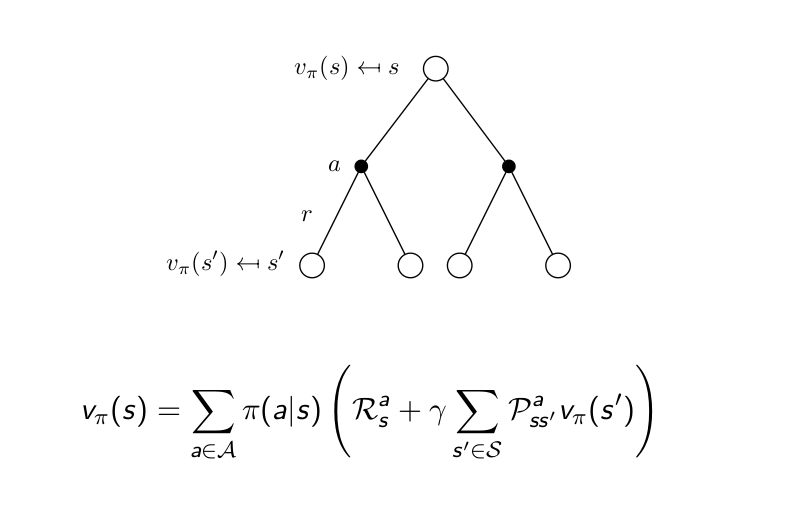
실재 강화학습으로 무엇인가를 학습시킬 때 reward와 state transition probability는 미리 알 수가 없습니다. 경험을 통해서 알아가는 것 입니다. 이러한 정보를 다 알면 MDP를 모두 안다고 표현하며 이러한 정보들이 MDP의 model이 됩니다. 강화학습의 큰 특징은 바로 MDP의 model를 몰라도 학습할 수 있다는 것 입니다. 따라서 reward function과 state transition probability를 모르고 학습하는 강화학습에서는 Bellman equation으로는 구할 수가 없습니다.
Bellman equation for Q-function
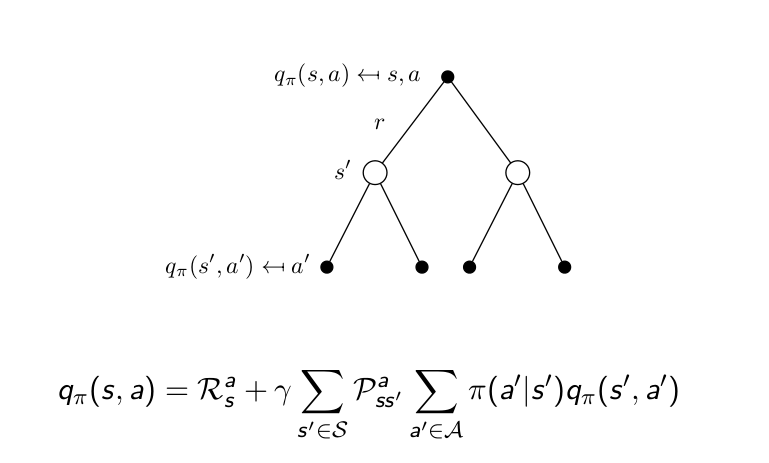
같은 식을 action value function에 대해서 작성하고 그림을 보면 다음과 같습니다.
Continuous-time optimization problem
보통 우리가 부르는 Bellman equation은 뒤에서 언급될 dynamic programming같이 discrete한 time에서의 최적화 문제에 적용되는 식을 의미합니다. 하지만 시간이 연속적인 문제의 경우에는 Hamilton–Jacobi–Bellman equation이라고 부르는 식이 따로 있습니다. 관련 내용은 아래 홈페이지를 참고해주시길 바랍니다.
https://en.wikipedia.org/wiki/Bellman_equation