Eligibility Traces

n-step TD나 TD($$\lambda$$), eligibility trace는 최근 강화학습에서 많이 다루는 알고리즘들은 아닙니다. 하지만 최근 Asynchronous methods for deep reinforcement learning 논문에서 n-step을 사용한 일은 있었습니다. 하지만 제가 생각하기에 크게 중요한 부분은 아니고 "어떠한 문제점이 있어서 개선시키려고 했던 과정들이구나"라고 생각하면 편할 것 같습니다.

1. n-step TD

TD learning은 Monte-Carlo learning에 비해서 매 time-step마다 학습을 할 수 있다는 장점이 있었습니다. 다시 한 번 TD Control인 Sarsa를 봐보겠습니다. 아래의 update식을 보면 결국 update한 번 할 때 R하나의 정보밖에 알 수 없어서 학습하는데 오래걸리기도 하고 bias가 높기 때문에 사실은 TD와 MC의 둘의 장점을 다 살릴 수 있다면 좋습니다.

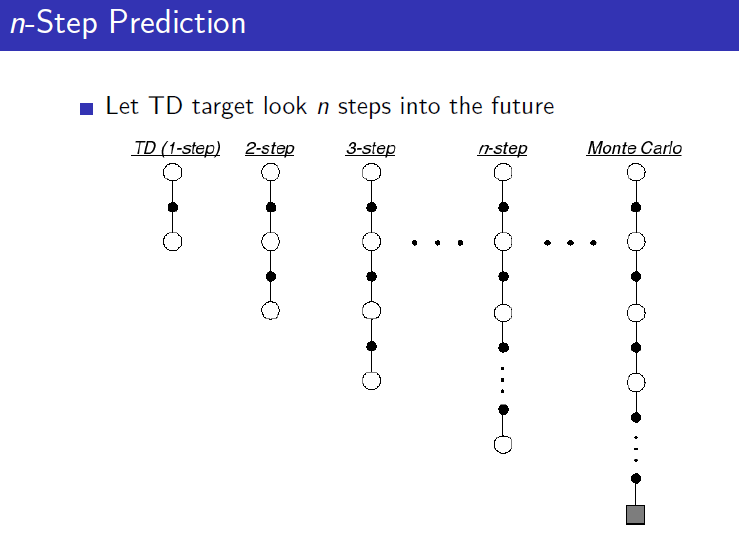
따라서 update를 할 때 one step만 보고서 update를 하는 것이 아니고 n-step을 움직인 다음에 update를 하자라고 생각하게 됩니다. 만약 지금이 t라고 하면 t+n이 되면 그 때까지 모았던 reward들로서 n-step return을 계산하고 그 사이의 방문했던 state들의 value function을 update하는 것입니다. 그것이 바로 n-step TD입니다. 몇 개의 time-step마다 update를 할 건지는 자신이 결정하면 됩니다. 이 n-step이 terminal state까지 간다면 그게 바로 Monte-Carlo이 됩니다. 따라서 둘의 장점을 다 취하기 위해서 그 사이의 적당한 n-step을 선택해주는 것이 좋습니다. 하지만 어떻게 적당한 n-step이라는 것을 알 수 있고 그 기준이 무엇일까요??

2. Forward-View of TD($$\lambda$$)

Random walker라는 prediction example입니다. C state에서 시작해서 왼쪽 오른쪽으로 random하게 움직이는 policy를 가지고 있습니다. 이 문제에 대한 true value function 아래 그래프에 그려진 것처럼 되어있고 저 value function을 experience를 통해서 찾아내야합니다.

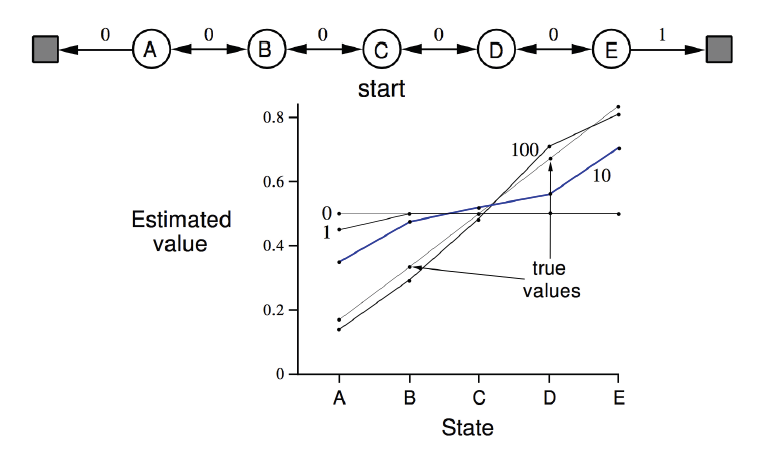
이 문제에 n-step TD prediction을 적용시켜볼 경우에 n으로 적당한 숫자가 얼마인지 판별하기 쉽지 않습니다. 아래 그래프는 x축은 $$\alpha$$, y축은 true value function과의 error입니다. 아래 그래프와 같이 $$\alpha$$의 값에 따라서 어떤 n-step이 학습에 좋은지는 달라지기 때문에 사실은 여러 n-step TD를 합할 수 있다면 각 n의 장점을 다 취할 수 있을 것입니다.

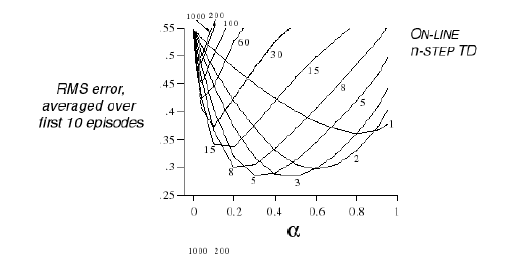
따라서 이 모든 n-step return을 모두 더해서 사용하기로 하였습니다. 하지만 단순히 더해서 평균을 구하는 방식이 아니고 아래와 같이 $$\lambda$$라는 weight를 사용해서 geometrically weighted sum을 이용합니다. 이렇게 하면 모든 n-step을 다 포함하면서 다 더하면 1이 나옵니다. 이것을 통해서 구한 $$\lambda$$-return을 원래 MC의 return자리에 넣어주면 forward-view TD($$\lambda$$)가 됩니다.

이것을 그림으로 나타내자면 다음과 같습니다.

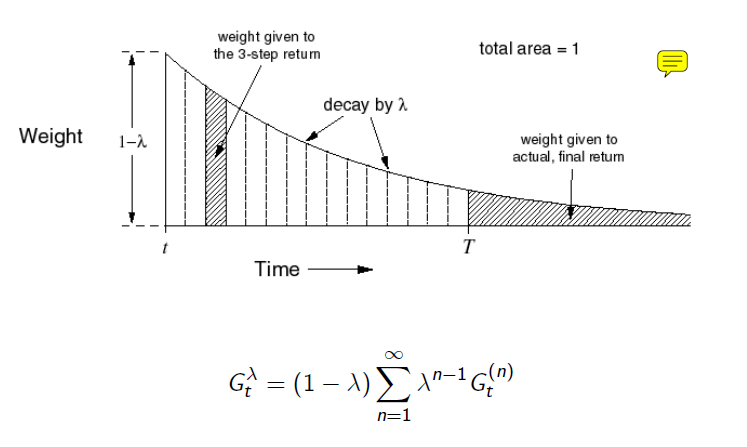
다시 정리를 해보자면 TD는 time-step마다 학습할 수 있는 장점은 있었지만 또한 bias가 높고 학습정보가 별로 없기 때문에 TD와 MC의 장점을 둘 다 살리기 위한 방법으로 n-step TD가 있었습니다. 하지만 각 n-step이 상황마다 다른 장점이 있어서 이 모든 장점을 포함하기 위해서 $$\lambda$$라는 weight를 도입해서 $$\lambda$$-return을 계산해서 사용하는 것이 forward-view TD($$\lambda$$)입니다. 하지만 이 방법에도 단점이 있습니다. 바로 MC와 똑같이 episode까 끝나야 update를 할 수 있다는 것입니다.(모든 n-step을 포함하니까)

3. Backward-View of TD($$\lambda$$)

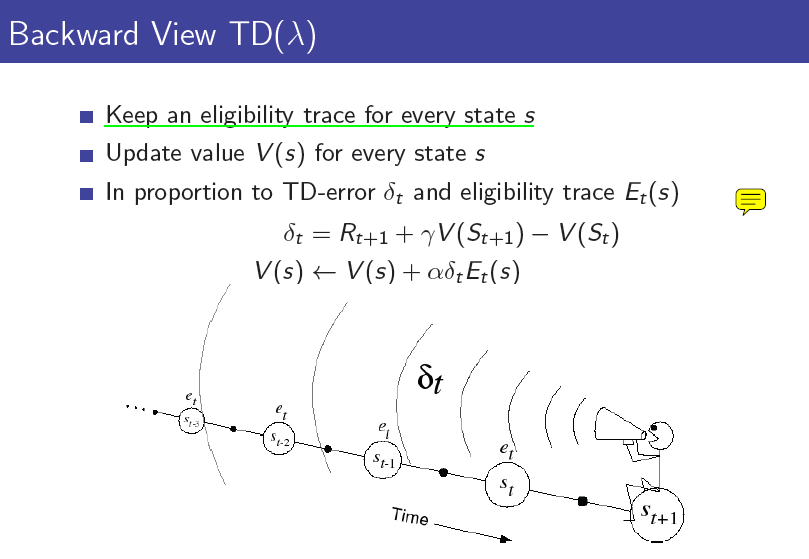
따라서 본래 TD의 장점이었던 time-step마다 update할 수 있다는 장점이 사라졌습니다. MC의 장점은 살리면서도 바로 바로 update할 수 있는 방법이 없을까요? 여기서 바로 eligibility trace라는 개념이 나옵니다. 아래 그림과 같이 과거에 있었던 일들 중에서 현재 내가 받은 reward에 기여한 것이 무엇일까?라는 credit assignment문제에서 "얼마나 최근에 일어났던 일이었나"와 "얼마나 자주 발생했었나"라는 것을 기준으로 과거의 일들을 기억해놓고 현재 받은 reward를 과거의 state들로 분배해주게 됩니다.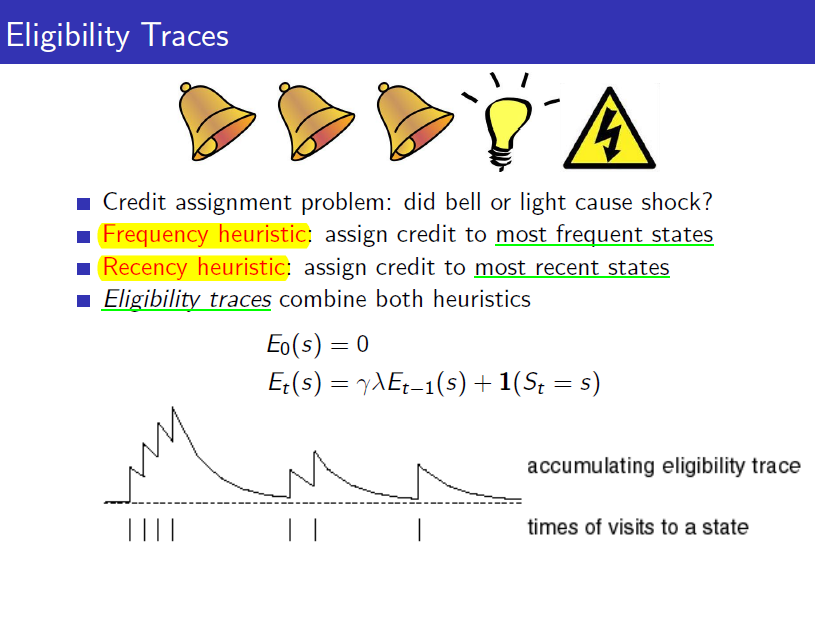
즉 TD(0)처럼 현재 updaate할 $$\delta$$를 계산하면 현재의 value function만 update하는 것이 아니라 과거에 지나왔던 모든 state에 eligibility trace를 기억해두었다가 그 만큼 자신을 update하게 됩니다. 따라서 아래 그림과 같이 현재의 경험을 통해 한 번에 과거의 모든 state들의 value function을 update하게 되는 것입니다. 현재의 경험이 과거의 value function에 얼마나 영향을 주고 싶은가는 $$\lambda$$를 통해 조절할 수 있습니다. 이러한 update 방식을 backward-view TD($$\lambda$$)라고 합니다.

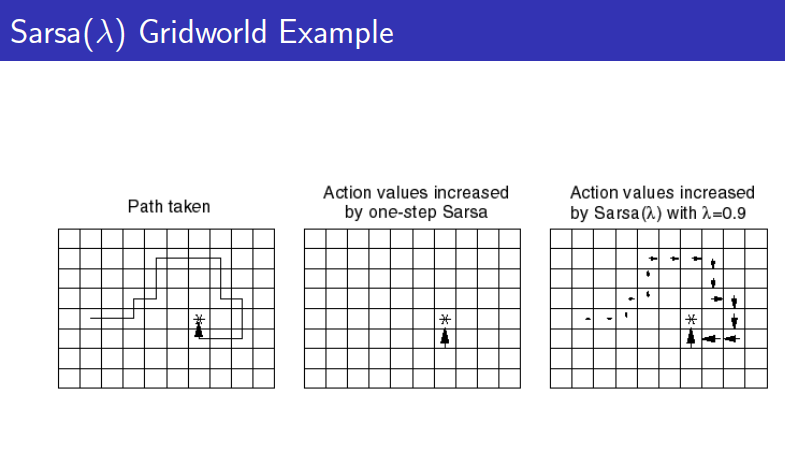
4. Sarsa($$\lambda$$)

위에서는 TD prediction만 다루었습니다. 여기서는 TD Control에 대해서 다루도록 하겠습니다. Sarsa에도 n-step Sarsa가 있고 forward-view Sarsa($$\lambda$$)가 있고 backward-view Sarsa($$\lambda$$)가 있습니다. 각 각은 다음과 같습니다. 설명은 생략하겠습니다.

backward-view Sarsa($$\lambda$$)를 algorithm으로 표현하자면 아래과 같습니다.

또한 Eligibility trace를 이론으로만 봐서 이해가 안가는 분들이 계실텐데 아래 그림을 보면 이해가 쉽습니다. Path taken을 보면 지금까지 지나왔던 곳에 대해서 각 각의 eligibility trace를 기억해놨다가 어느 지금에 이르러서 reward를 얻어서 update를 하려하면 자동으로 과거에 지나왔던 모든 state의 value function이 함께 update가 됩니다.