Markov Decision Process

David Silver 강의에서는 MDP를 배우기 전에 Markov하다는 말의 정의와 Markov Chain, Markov Reward Process를 배웁니다. Markov는 1800년대의 러시아 수학자의 이름입니다. 이 분의 이름이 하나의 형용사가 되었는데 그 의미는 다음과 같습니다.

뒤에서 state와 value에 대해서 설명하겠습니다.

위의 첫 식처럼 처음 어떠한 상태로부터 시작해서 현재 상태까지 올 확률이 바로 전 상태에서 현재 상태까지 올 확률과 같을 때, 두 번째 식처럼 표현이 될 수 있고 state는 Markov하다고 일컬어질 수 있습니다.

스타크래프트같은 게임이라고 생각하면 게임 중간 어떤 상황은 이전의 모든 상황들에 영향을 받아서 지금의 상황이 된 것이기 때문에 사실은 지금 상황에 이전 상황에 대한 정보들이 모두 담겨있다고 가정할수도 있습니다. 강화학습이 기본적으로 MDP로 정의되는 문제를 풀기때문에 state는 Markov라고 가정하고 접근합니다. 하지만 절대적인 것은 아니며 Non-Markovian MDP도 있으며 그러한 문제를 풀기위한 강화학습들도 있지만 상대적으로 연구가 덜 되었으며 처음에 접하기에는 적합하지 않습니다. 강화학습에서는 value라는 어떠한 가치가 현재의 state의 함수로 표현되고 이 state가 Markov하다고 가정됩니다.

다음은 UC Berkeley의 intro to AI 강의의 slide에서 가져온 그림입니다.
http://ai.berkeley.edu/lecture_slides.html

위 그림에서 로봇이 세상을 바라보고 이해하는 방식이 MDP가 됩니다. MDP란 Markov Decision Process의 약자로서 state, action, state transition probability matrix, reward, discount factor로 이루어져있습니다. 로봇이 있는 위치가 state, 앞뒤좌우로 이동하는 것이 action, 저 멀리 보이는 빛나는 보석이 reward입니다. 한 마디로 문제의 정의입니다. 이제 이 로봇은 보석을 얻기 위해 어떻게 해야할지를 학습하게 될 것 입니다. 그 전에 MDP에 대해서 더 살펴볼 필요가 있습니다.

다시 제가 들었던 Silver교수님의 강의에서 말하는 MDP의 정의를 살펴보겠습니다. 밑의 그림은 http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html
에 있는 2장 자료에서 가져왔습니다.

State

간단히 설명을 하자면 state는 agent가 인식하는 자신의 상태입니다. 사람으로 치자면 눈이라는 관측도구를 통해서 "나는 방에 있어"라고 인식하는 과정에서 "방"이 state가 됩니다.

이 이외에도 state는 생각보다 많은 것들이 될 수 있는데 달리는 차 같은 경우에는 "차는 Jeep이고 사람은 4명 탔으며 현재 100km/h로 달리고 있다"라는 것이 state가 될 수 있습니다. OpenAI에도 있는 atari game같은 경우에는 게임화면 자체, 즉 pixel이 agent가 인식하는 state가 됩니다. 또 Cartpole에서는 cart의 x위치와 속도, pole의 각도와 각속도가 state가 됩니다. 즉, 문제는 정의하기 나름입니다. 실재로 어떠한 문제를 강화학습으로 풀 수도 있고 다른 machine learning 기법으로 풀 수도 있기 때문에 강화학습을 적용시키기 전에 왜 강화학습을 써야하고 다른 머신러닝 기법에 비해서 나은 점이 무엇인가를 따져보고 사용해야할 것 같습니다. 강화학습은 "시간"이라는 개념이 있는 문제를 푸는 인공지능 기법입니다. 이는 결국 강화학습의 목표가 Policy(일련의 행동들)된다는 의미를 함포합니다.

Action

Agent의 역할은 무엇일까요? environment에서 특정 state에 갔을 때 action을 지시하는 것입니다. robot이 왼쪽으로 갈지, 오른쪽으로 갈 지를 결정해주는 역할입니다. 그래서 사람의 뇌라고 생각하면 이해가 쉽습니다. "오른쪽으로 간다", "왼쪽으로 간다"라는 것이 action이 되고 agent가 그 action를 취했을 경우에 실재로 오른쪽이나 왼쪽으로 움직이게 됩니다. 또한 agent는 action을 취함으로서 자신의 state를 변화시킬 수 있습니다. 로봇에서는 흔히 Controller라 부르는 개념입니다.

State transition probability matrix

robot이 움직인다고 생각해봅시다. robot이 왼쪽으로 움직이면 위치가 변하듯이, action을 취하면 environment상의 agent의 state가 변하는 데 그것 또한 environment가 agent에게 알려줍니다. 정확히 말하면 agent가 observe하는 것 입니다. 대신에 어떠한 외부요인에 의해 (ex 바람이 분다던지) robot이 왼쪽으로 가려했지만 오른쪽으로 가는 경우가 발생할 수 있습니다. 다음 그림을 참고하면 개념이 좀 더 잘 와 닿으실 겁니다. 로봇은 앞으로 간다고 갔지만 왼쪽으로 가서 불에 빠질 수도 있고 오른쪽으로 갈 수도 있다는 것입니다. 그 확률을 표현하는 것이 "state transition probability matrix"입니다. 이렇게 어떠한 action을 취했을 경우 state가 deterministic하게 딱 정해지는 것이 아니고 확률적으로 정해지게 되는데 일종의 noise라고 생각하셔도 될 것 같습니다.

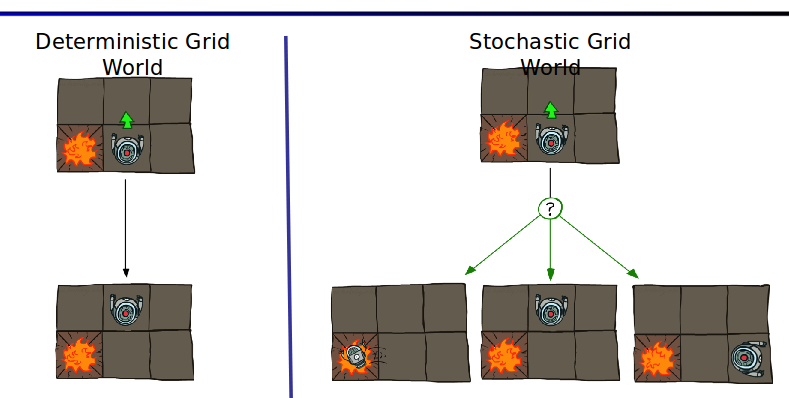
정의는 다음과 같습니다. s라는 state에서 a라는 행동을 취할 때 s'에 도착할 확률을 이야기합니다.

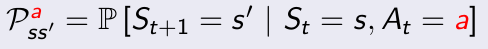
Markov Chain

MDP에서 action과 reward가 없다고 가정해봅시다. 그렇다면 state와 state끼리의 transition matrix를 생각해볼 수 있을 것 입니다. Silver교수님은 Markov Chain에 대해서 다음과 같이 설명하셨습니다. 학생들의 상태를 state로 잡고 각 state끼리의 transition probability를 정의할 수 있습니다. 이것만으로서는 무엇인가를 학습시킬 수 없지만 MDP를 배우기전에 배우는 기본 개념으로서 유용한 것 같고 후에 policy gradient에서 다루는 stationary distribution을 이해하는데 도움이 될 것 같습니다. 이 Markov Chain에서는 무한대로 시간이 흐르면 모두 Sleep으로 수렴할 것이고 더이상 변화가 없기 때문에 stationary distribution이라고 말합니다. 현재는 어떤 state에서 state로 가는 확률이 표시되어 있지만 MDP에서는 action을 할 확률과 action을 해서 어떤 state로 갈 확률이 주어지게 됩니다.

Reward

agent가 action을 취하면 그에 따른 reward를 "environment"가 agent에게 알려줍니다. 그 reward는 atari game에서는 "score", 바둑의 경우에는 승패( 알파고가 학습하는 방법), trajectory control의 경우에는 "의도한 궤도에 얼마나 가깝게 움직였나"가 됩니다. 정의는 다음과 같습니다. s라는 state에 있을 때 a라는 action을 취했을 때 얻을 수 있는 reward입니다. 강화학습에서는 정답이나 사전에 환경에 대한 지식이 없이 이 reward를 통해서 agent가 학습하게 됩니다.

이 reward를 immediate reward라고 하는데 agent는 단순히 즉각적으로 나오는 reward만 보는 것이 아니라 이후로 얻는 reward들까지 고려합니다.

Discount Factor

reward의 정의에 따라 각 state에서 어떠한 action을 취하면 reward를 받게 되는데 이때 단순히 받았던 reward들을 더하면 다음과 같은 문제가 발생합니다.

• 어떠한 agent는 각 time-step마다 0.1씩 reward를 받고 다른 agent는 1씩 받았을 경우에 시간이 무한대로 흘러간다면 0.1씩 계속 더해도 무한대이고 1씩 계속 더해도 무한대입니다. 수학에서 무한대는 크기 비교를 할 수 없습니다.

• 다음 두 가지 경우를 구분 할 수가 없습니다. agent가 episode를 시작하자마자 1 받았을 경우와 끝날 때 1을 받았을 경우를 둘 다 전체 reward를 1을 받았기 때문에 두 상황중에 어떤 경우가 더 나은 건지를 판단할 수 없습니다.

따라서 discount factor라는 개념이 등장하게 됩니다. 사람의 입장에서 생각해보면 당장 지금 배고픈 것을 채우는 것이 내일 배고픈 것을 채우는 것보다 중요하다 생각하고 행동하는 것처럼 discount factor를 통해서 시간에 따라서 reward의 가치가 달라지는 것을 표현하는 것 입니다. discount factor는 0에서 1 사이의 값 입니다. 다음 그림을 보면 이해가 쉽습니다.

제가 이해하기로는 discount factor가 0이면 상당히 근시안적인 것이고 discount factor가 1이면 상당히 미래지향적인 것이라서 사실은 사람이 어떤 행동을 결정할 때 미래를 생각하며 결정하긴 하지만 모든 미래에 일어날 일을 다 고려하지는 않습니다. 따라서 dicount factor는 보통 0에서 1사이의 값을 사용합니다.

Agent-Environment Interface

이렇듯 agent는 action을 취하고 state를 옮기고 reward를 받고 하면서 environment와 상호작용을 하는데 그 그림은 다음과 같습니다.

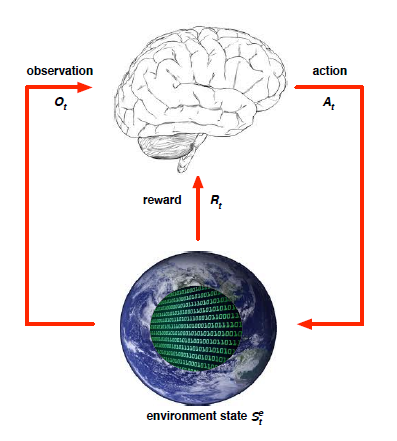
agent가 observation을 통해서 자신의 state를 알게되면 그 state에 맞는 action을 취하게 됩니다. 학습을 하지 않은 초기에는 random action을 취합니다. 그러면 environment가 agent에게 reward와 다음 state를 알려주게 됩니다. 시뮬레이터나 게임이 environment가 될 수도 있고 실재 세상이 environment가 될 수도 있습니다.

Policy

뜻 그대로 풀이하자면 "정책"입니다. 위에서 말했듯이 agent는 어떤 state에 도착하면 action을 결정하는 데 어떤 state에서 어떤 action을 할 지를 policy라고 합니다. 결국에 강화학습의 목적은 optimal policy ( accumulative reward = return 을 최대화하는 policy)를 찾는 것입니다(이것이 잘못된 관념이라고 얘기하는데 실재로 Policy Gradient는 suboptimal에 빠질수 있지만 강화학습입니다). policy의 정의는 다음과 같습니다. state s에서 aciton a를 할 확률을 이야기합니다.

MDP Graph

Markow Decision Process는 다음과 같이 그래프로 나타낼 수 있습니다. 이번에도 student의 수업을 듣는 것을 예로 들어서 Silver 교수님이 설명했습니다. 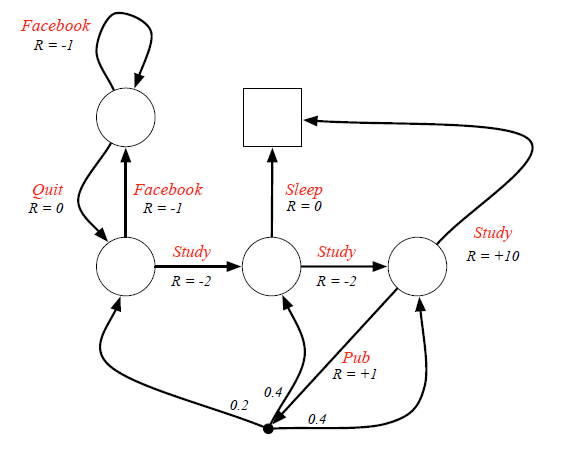이와 같이 MDP의 graph는 state 사이의 transition 대신에 action을 통한 state의 transition과 reward로서 표현되게 됩니다.