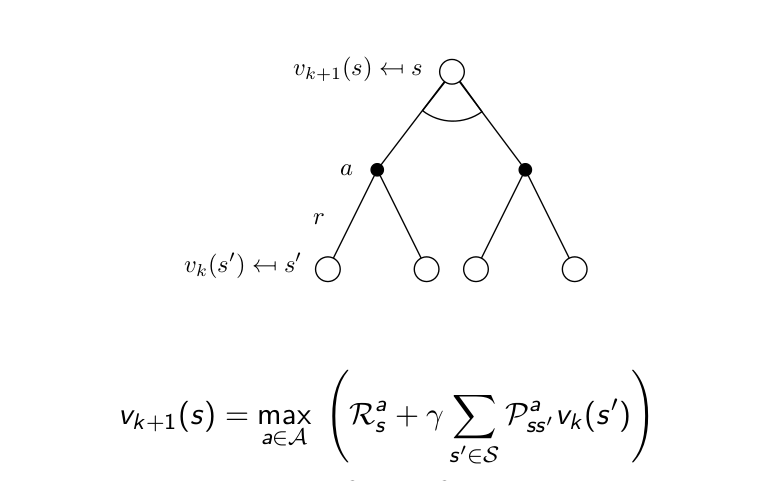
Value Iteration
Value Iteration
Value Iteration이 Policy Iteration과 다른 점은 Bellman Expectation Equation이 아니고 Bellman Optimality Equation을 사용한다는 것입니다. Bellman Optimality Equation은 optimal value function들 사이의 관계식입니다. 단순히 이 관계식을 iterative하게 변환시켜주면 됩니다. Policy Iteration의 경우에는 evaluation 할 때 수많은 계산을 해줘야하는 단점이 있었는데 그 evaluation을 단 한 번만 하는 것이 value iteration입니다. 따라서 현재 value function을 계산하고 update할 때 max를 취함으로서 greedy하게 improve하는 효과를 줍니다. 따라서 한 번의 evaluation + improvement = value iteration이 됩니다.
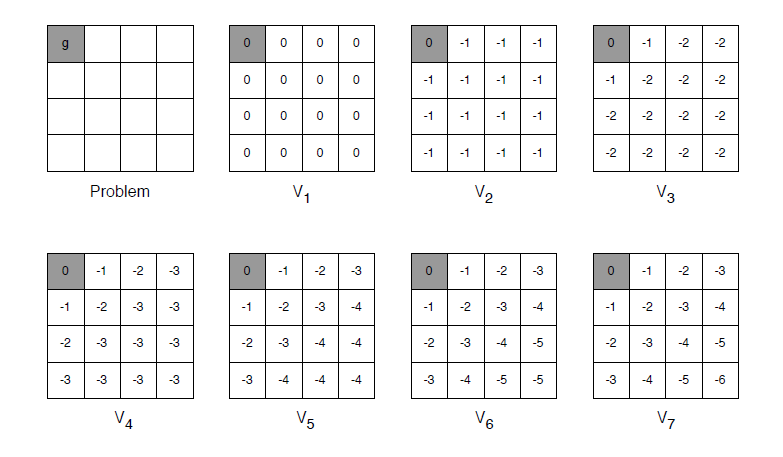
value iteration의 예를 살펴봅시다. 아래 그림은 terminal state가 하나인 gridworld이고 time step이 지나갈 때마다 -1의 reward를 받는 environment입니다. 아래 그림은 value iteration의 iteration숫자가 하나씩 늘어갈 때 각 state의 value function을 표시한 것 입니다. 변하지 않는 듯이 보이는 state들이 있지만 사실 같은 값으로 계속 update되고 있는 것입니다. V2의 (2,1)state의 value function -1을 보면
V2 = max(-1 + V(주변)) = -1
max를 취하고 terminal state가 계속 0의 value function을 가지기 때문에 (2,1) state는 계속 같은 값으로 업데이트가 됩니다. 그 이후로도 이와 같이 iteration을 진행하면 optimal value function을 구할 수 있고 그로 인해 optimal policy도 구할 수 있습니다.
Sample Backup
이렇게 Dynamic Programming에 대해서 살펴보았습니다. 처음에 언급했다시피 DP는 MDP에 대한 정보를 다 가지고 있어야 optimal policy를 구할 수 있습니다. 또한 DP는 full-width backup(한 번 update할 때 가능한 모든 successor state의 value function을 통해 update하는 방법)을 사용하고 있기 때문에 단 한 번의 backup을 하는 데도 많은 계산을 해야합니다. 또한 위와 같은 작은 gridworld 같은 경우는 괜찮지만 state 숫자가 늘어날수록 계산량이 기하급수적으로 증가하기 때문에 MDP가 상당히 크거나 MDP에 대해서 다 알지 못할 때는 DP를 적용시킬 수 없습니다.

이때 등장하는 개념이 sample back-up입니다. 즉, 모든 가능한 successor state와 action을 고려하는 것이 아니고 Sampling을 통해서 한 길만 가보고 그 정보를 토대로 value function을 업데이트한다는 것입니다. 이렇게 할 경우 계산이 효율적이라는 장점도 있지만 "model-free"가 가능하다는 특징이 있습니다. 즉, DP의 방법대로 optimal한 해를 찾으려면 매 iteration마다 Reward function과 state transition matrix를 알아야 하는데 sample backup의 경우에는 아래 그림과 같이 <S,A,R,S'>을 training set으로 실재 나온 reward와 sample transition으로서 그 두 개를 대체하게 됩니다. 따라서 MDP라는 model을 몰라도 optimal policy를 구할 수 있게 되고 "Learning"이 되는 것 입니다. sample이라면 개념이 좀 어렵게 다가올 수도 있는데 처음에 강화학습이 trial and error로 학습한다 했던 것을 떠올려서 sample이 하나의 try라고 생각하면 이해가 잘 될 것 같습니다. 즉, 머리로 다 계산하고 있는 것이 아니고 일단 가보면서 겪는 experience로 문제를 풀겠다는 것입니다. DP를 sampling을 통해서 풀면서부터 "Reinforcement Learning"이 시작됩니다.
